Ποιος είναι ο Κωνσταντίνος Καραθεοδωρή;

O Κωνσταντίνος Καραθεοδωρή, αποτελεί ένα από τα σημαντικότερα πρόσωπα παγκοσμίως στη μαθηματική επιστήμη και τη θεωρητική φυσική, αλλά και  πρόσωπο- ορόσημο για την ελληνική επιστημονική κοινότητα.  Το επιστημονικό του έργο επεκτείνεται σε πολλούς τομείς των Μαθηματικών και της Φυσικής και της Αρχαιολογίας. Είχε σημαντικότατη συνεισφορά στους τομείς της πραγματικής ανάλυσης, συναρτησιακής ανάλυσης και θεωρίας μέτρου και ολοκλήρωσης.

Γεννήθηκε στο Βερολίνο το 1873 και το 1891 εγγράφεται στη Στρατιωτική Σχολή του Βελγίου (Ecole Militaire de Belgique), από την οποία αποφοιτά ως πολιτικός μηχανικός.

Το φθινόπωρο του 1898 μεταβαίνει στην Αίγυπτο καθώς είχε προσληφθεί ως βοηθός μηχανικός, από τη Βρετανική εταιρεία που κατασκεύαζε τα φράγματα του Ασουάν και του Ασιούτ. Ο ελεύθερός του χρόνος αφιερωνόταν στη μελέτη επιφανών μαθηματικών όπως ο C. Jordan και ο Salmon-Fiedler, ενώ παράλληλα μελετούσε την κατασκευή των πυραμίδων.  Λίγα χρόνια μετά αποφασίζει να εγκαταλείψει το επάγγελμα του μηχανικού και να αφοσιωθεί στο θαυμαστό κόσμο των μαθηματικών ο οποίος τον γοήτευε πάντα.

Παρακολούθησε για δύο χρόνια μαθήματα στο Πανεπιστήμιο του Βερολίνου και συνέχισε τις σπουδές του στο Πανεπιστήμιο το Γκέτινγκεν (Goetingen), που την εποχή εκείνη ήταν το μεγαλύτερο ερευνητικό κέντρο Μαθηματικών της Ευρώπης. Από το πανεπιστήμιο αυτό πήρε διδακτορικό δίπλωμα το 1904 και τον τίτλο του υφηγητή το 1905. Αφού διετέλεσε καθηγητής για σύντομα χρονικά διαστήματα σε δύο περιφερειακά πολυτεχνεία της Γερμανίας, το 1913 εκλέγεται καθηγητής στο Πανεπιστήμιο του Γκέτινγκεν και το 1918 καθηγητής στο Πανεπιστήμιο του Βερολίνου.

Οι έρευνες του, τις οποίες δημοσίευσε κυρίως στα γερμανικά, συνθέτουν ένα τεράστιο και πολύπλευρο έργο, το οποίο τον κατατάσσει μεταξύ των μεγαλύτερων μαθηματικών. Αρχικά ασχολήθηκε με τον Λογισμό των Μεταβολών και η διδακτορική διατριβή του (Γκέτινγκεν, 1904) φέρει τον τίτλο «Περί των ασυνεχών λύσεων στον Λογισμό των Μεταβολών». Στην συνέχεια, καταπιάστηκε με όλους σχεδόν του κλάδους των Μαθηματικών: θεωρία πραγματικών συναρτήσεων, θεωρία μιγαδικών συναρτήσεων, διαφορικές εξισώσεις, θεωρία συνόλων και διαφορική γεωμετρία, σύμμορφες απεικονίσεις κ.ά.

Σημαντική θεωρείται και η συμβολή του στην Θεωρητική Φυσική, με μαθηματική θεμελίωση τομέων της Φυσικής όπως η Θερμοδυναμική, η Γεωμετρική Οπτική, η μηχανική και η Σχετικότητα.

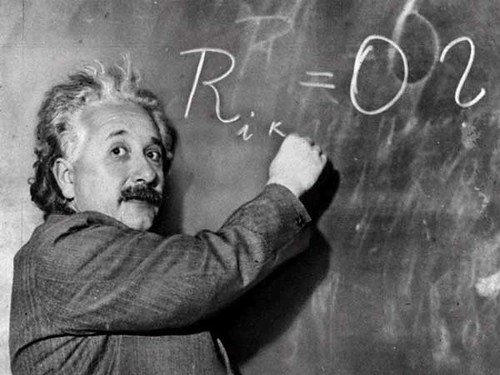
Στα πλαίσια αυτής της σημαντικής ερευνητικής του πορείας έρχεται σε επαφή με μεγάλους επιστήμονες της εποχής, ανάμεσα στους οποίους και ο Άλμπερτ Αϊνστάιν, ο οποίος δείχνοντας ενδιαφέρον για τις μαθηματικές αποδείξεις του Καραθεοδωρή στο Λογισμό των Μεταβολών γράφει σε επιστολή του το 1916: 

«Αν θέλετε να μπείτε στον κόπο να μου εξηγήσετε ακόμα και τους κανονικούς μετασχηματισμούς θα βρείτε έναν ευγνώμονα και ευσυνείδητο ακροατή. Αν όμως λύσετε και το πρόβλημα των κλειστών γραμμών του χρόνου, θα σταθώ μπροστά σας με σταυρωμένα χέρια. Πίσω από αυτό υπάρχει κρυμμένο κάτι που είναι αντάξιο του ιδρώτα των καλυτέρων.» 

Οι επιστολές που ανταλλάσσουν οι δύο τους είναι αρκετές επισφραγίζοντας έτσι μια επιστημονική σχέση στηριγμένη στην αλληλοεκτίμηση και το σεβασμό.  

Κάποιοι ισχυρίζονται πως η  μαθηματική σκέψη του Καραθεοδωρή επηρέασε τον Αϊνστάιν στην ανάπτυξη της Γενικής Θεωρίας της Σχετικότητας, κάποιοι πάλι θεωρούν πως ο Καραθεοδωρή δεν είχε καμία ανάμιξη στη διαμόρφωση της θεωρίας.

Για όλους εμάς όμως δεν πρέπει να έχει σημασία αν ο Καραθεοδωρή έχει “μερίδιο” στην διατύπωση της Γενικής Θεωρίας της Σχετικότητας και αν  επηρέασε ή όχι τη διαμόρφωση της σκέψης του Αϊνστάιν.

Αυτό που κρατάμε σε κάθε περίπτωση είναι πως οι δύο αυτοί μεγάλοι επιστήμονες μέσα από την μεταξύ τους επικοινωνία κατάφεραν να αλληλεπιδρούν και να συνδιαμορφώνουν απόψεις και θεωρίες, η σημαντικότητα των οποίων επηρεάζει πολλές περισσότερες εκφάνσεις της καθημερινότητας μας απ’ ότι νομίζουμε. 

«Εάν θέλεις να φτάσεις έως το άπειρο, γνώρισε το πεπερασμένο σε όλες τις εκφράσεις του» , (Κων/νος Καραθεοδωρή)

 

Βασιλική Μπέσιου

Πηγή: TEDxAthens